一种应用于云平台负载的PID非线性控制系统设计
本文的实现效率尚有待考证，极有可能沦为扯淡文，但如果在网络资源部分可以快速应用测试。
众所周知，很多计算机系统里的设计都可以描述为线性模型，但正如金融系统的发展，计算机系统直接面向大众以后，也会呈现出非线性的特征，比如典型的DDoS即是在系统设计之外。接下来，笔者将使用自控知识来设计一种自适应负载的云计算控制器，不仅适用于计算、也会适用于网络、存储等服务资源。
以OpenStack平台的计算（虚拟机）为例，当用户的计算需求被量化后，那么我们就能根据其需求直接给出相应数量的计算节点。假如用户的计算需求是变化的，其值为R，且我们的程序员也是个直肠子，给出相应的计算能力为C，那么他设计的程序很有可能就是这个公式：
N=10, R=nN, C=(n+2)N
每台虚拟机的计算能力N为10，虚拟机数量为n。
可以看出他给了两台的冗余量，啊哈，还不错。所以他期望的场景应该是这样的。
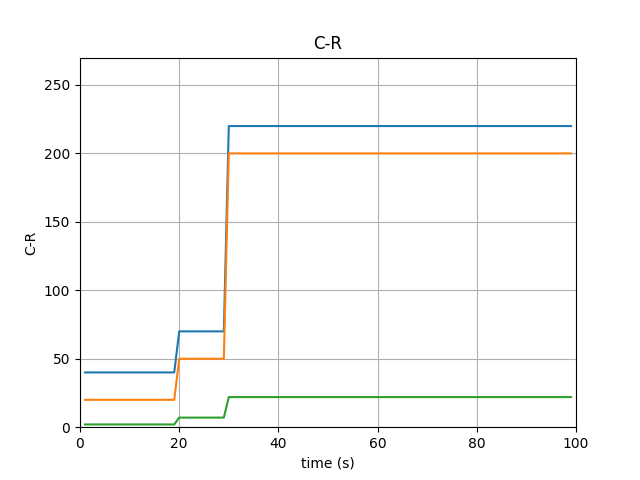
其中黄色为实际需求，蓝色为平台提供,绿色为虚拟机数量。
但是，假如需求呈现出短时间大量波动的话，比如下图。
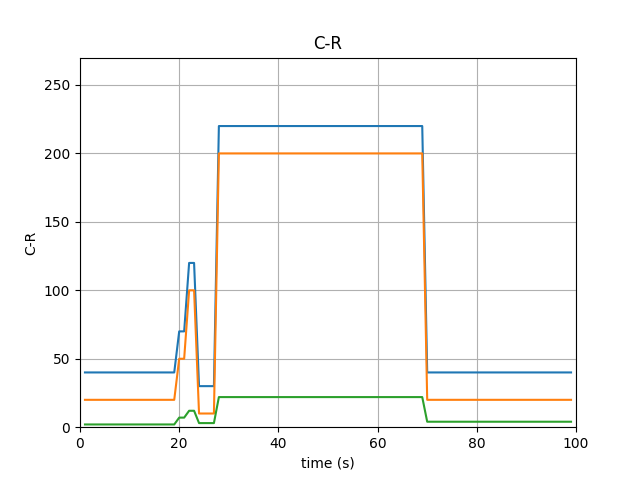这个时候事情就不是那么美妙了，平台在即时响应的同时，伴随着大量虚拟机的上线/下线，从而造成一定的资源请求拥堵，降低控制性能。
接下来，我们尝试引入PID回馈控制器，就是这个样子的。
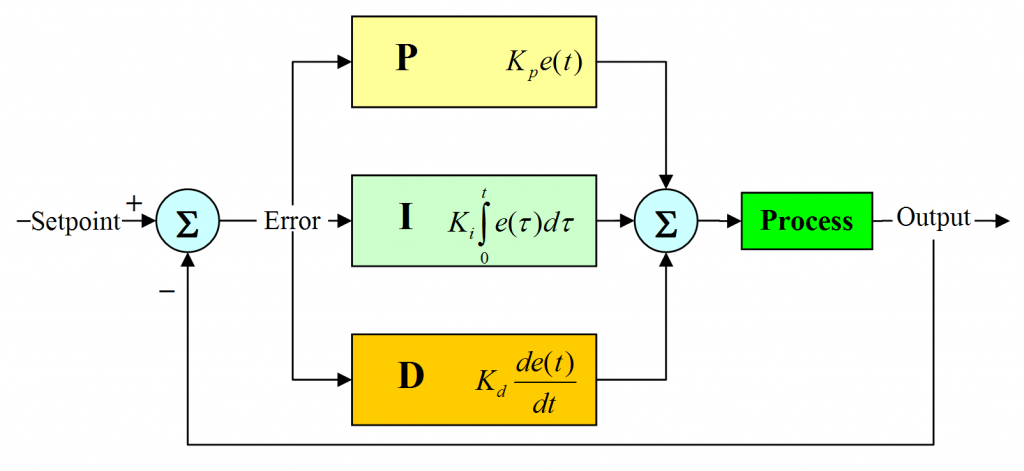
PID的Python代码实现如下：
!/usr/bin/python
import time
class PID: def init(self, P=0.2, I=0.0, D=0.0):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72 | self.Kp = P
self.Ki = I
self.Kd = D
self.sample_time = 0.00
self.current_time = time.time()
self.last_time = self.current_time
self.clear()
def clear(self):
#Clears PID computations and coefficients
self.SetPoint = 0.0
self.PTerm = 0.0
self.ITerm = 0.0
self.DTerm = 0.0
self.last_error = 0.0
# Windup Guard
self.int_error = 0.0
self.windup_guard = 20.0
self.output = 0.0
def update(self, feedback_value):
# Calculates PID value for given reference feedback
error = self.SetPoint - feedback_value
self.current_time = time.time()
delta_time = self.current_time - self.last_time
delta_error = error - self.last_error
if (delta_time >= self.sample_time):
self.PTerm = self.Kp * error
self.ITerm += error * delta_time
if (self.ITerm < -self.windup_guard):
self.ITerm = -self.windup_guard
elif (self.ITerm > self.windup_guard):
self.ITerm = self.windup_guard
self.DTerm = 0.0
if delta_time > 0:
self.DTerm = delta_error / delta_time
# Remember last time and last error for next calculation
self.last_time = self.current_time
self.last_error = error
self.output = self.PTerm + (self.Ki * self.ITerm) + (self.Kd * self.DTerm)
def setKp(self, proportional_gain):
# Determines how aggressively the PID reacts to the current error with setting Proportional Gain
self.Kp = proportional_gain
def setKi(self, integral_gain):
# Determines how aggressively the PID reacts to the current error with setting Integral Gain
self.Ki = integral_gain
def setKd(self, derivative_gain):
# Determines how aggressively the PID reacts to the current error with setting Derivative Gain
self.Kd = derivative_gain
def setWindup(self, windup):
# unwound
self.windup_guard = windup
def setSampleTime(self, sample_time):
# PID that should be updated at a regular interval.
self.sample_time = sample_time
|
然后在上图条件下进行PID控制，代码如下：
import PID import time import matplotlib.pyplot as plt import numpy as np from scipy.interpolate import spline
def test_pid(P = 0.2, I = 0.0, D= 0.0, L=100): """Self-test PID class
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62 | .. note::
...
for i in range(1, END):
pid.update(feedback)
output = pid.output
if pid.SetPoint > 0:
feedback += (output - (1/i))
if i>9:
pid.SetPoint = 1
time.sleep(0.02)
---
"""
pid = PID.PID(P, I, D)
pid.clear()
pid.SetPoint=0.0
pid.setSampleTime(0.01)
END = L
feedback = 0
feedback_list = []
time_list = []
setpoint_list = []
for i in range(1, END):
pid.update(feedback)
output = pid.output
if pid.SetPoint > 0:
feedback += (output - (1/i))
if i<10:
pid.SetPoint = 20
if i>20:
pid.SetPoint = 50
if i>22:
pid.SetPoint = 100
if i>24:
pid.SetPoint = 10
if i>28:
pid.SetPoint = 200
if i>30:
pid.SetPoint = 200
if i>70:
pid.SetPoint = 20
feedback_list.append(feedback)
setpoint_list.append(pid.SetPoint)
time_list.append(i)
time.sleep(0.02)
time_sm = np.array(time_list)
time_smooth = np.linspace(time_sm.min(), time_sm.max(), 300)
feedback_smooth = spline(time_list, feedback_list, time_smooth)
plt.plot(time_smooth, feedback_smooth)
plt.plot(time_list, setpoint_list)
plt.xlim((0, L))
plt.ylim((min(feedback_list)-0.5, max(feedback_list)+0.5))
plt.xlabel('time (s)')
plt.ylabel('PID C-R')
plt.grid(True)
plt.show()
|
if name == "main": test_pid(1.01, 1, 0.001, L=100)
然后看看现在是什么样呢？
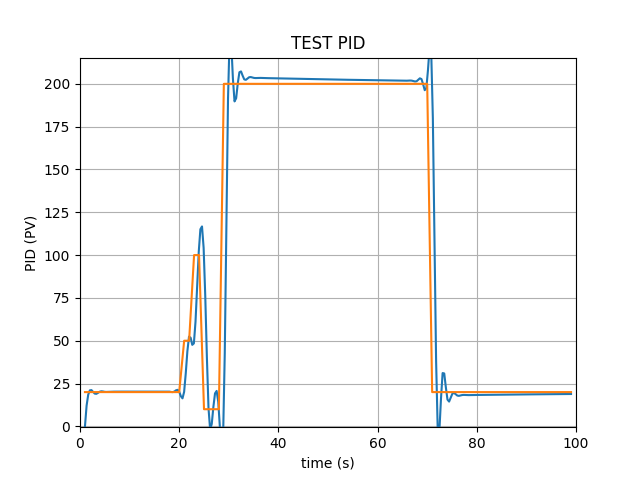
嗯，没错，多了一些调节量（超调量），且变化较之前平稳了一些。这些调节量是否适用于大批量的云计算环境还有待验证，但是以Web应用来看，这些调节量理应工作。
另外，考虑到虚拟机在创建后某些应用可能短时间内不接受下调，所以我们可以动态地调节C的值，即PID的输出仅用作参考。
这个时候事情就不是那么美妙了，平台在即时响应的同时，伴随着大量虚拟机的上线/下线，从而造成一定的资源请求拥堵，降低控制性能。
